गती व प्रकार (मोशन And Types)
या भागात आपल्याला भौतिकशात्त्र समजण्यासाठीच्या काही व्याख्या तसेच Basic Concepts पाहायच्या आहेत भौतिकशात्रात व्याख्या आणि त्यानूसार तयार झालेल्या सूत्रावर आधारित बऱ्याच संज्ञा स्पष्ट होतात.
महत्वाच्या संज्ञा व त्यांचा अर्थ
गती (Motion)
गती म्हणजे एखाद्या वस्तूने सभोवतालच्या वातावरणाशी आपली स्थिती बदलणे होय. जर एखादी वस्तू जागा बदलत असेल म्हणजेच ती गतिमान आहे असे म्हणता येईल आणि जर वस्तु जागा बदलण्याच्या स्थितीत नसेल तर त्या वस्तूला स्थिर वस्तू म्हणतात,
- गतीचे प्रमुख प्रकार
स्थानांतरणीय गती (Translational Motion)
आपणास माहिती आहे, गती म्हणजे जागा बदलण्याचा गुणधर्म.
जर एखादी वस्तू सरळ रेषेत किंवा थोडेफार वक्राकार स्वत:ची जागा बदलत असेल तर त्या गतीला ‘स्थानांतरणीय गती असे म्हणतात.
उदा.

घूर्णन गती (Rotational Motion)
ज्यावेळी एखाद्या वस्तूची गती ही एका विशिष्ट आसाभोवती (Axis) असेल, तर त्या गतीला घूर्णन गरती असे म्हणतात.
उदा. पंखा, भोवरा, पृथ्वीचे स्वत:भोवती फिरणे.
3.दोलन गती (Oscillatory Motion)
ज्या वस्तूची गती (हालचाल) पुन्हा पुन्हा एकाच मार्गाने होत असेल तर त्या गतीस “दोलन गती” असे म्हणतात.
उदा. दोलक, शिवणयंत्राची सुई, झोका.
विस्थापन आणि अंतर (Displacement & Distance)
अंतर (Distance)
अंतर म्हणजे गतिमान वस्तूमधील आरंभ बिंदू व अंतिम बिंदू यांच्यातील प्रत्यक्ष मार्गक्रमण होय.
विस्थापन (Displacement)
वस्तू स्थिर झाल्यानंतर आरंभ बिंदू व अंतिम बिंदू यांच्यातील कमीत कमी सरळ रेषेतील अंतर म्हणजेच”विस्थापन’ होय.
चाल व वेग (Speed & Velocity )
अ) चाल : (Speed)
एखाद्या वस्तूने एकक काळात कापलेल्या अंतरास “चाल” (Speed) असे म्हणतात.
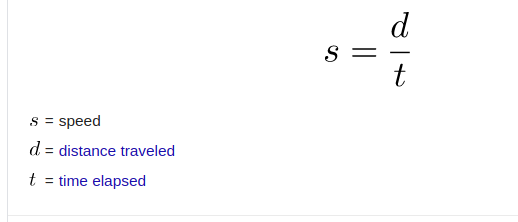
सूत्र: चाल =एकूण कापलेले अंतर/ एकूण लागलेला काळ
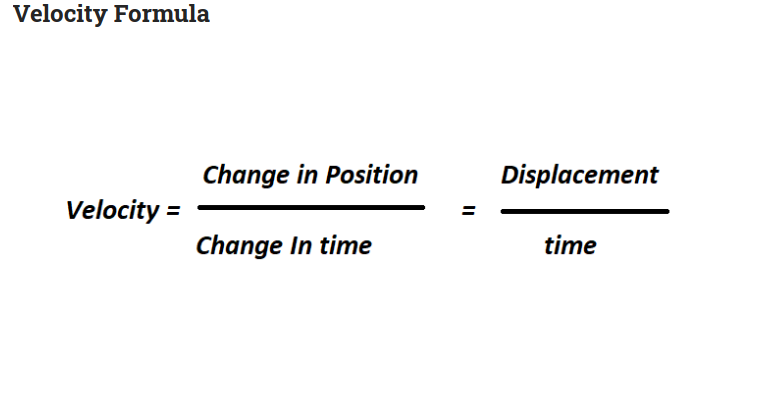
ब) वेग : (Velocity)
एखाद्या वस्तूने एकक काळात विशिष्ट दिशेने कापलेल्या अंतरास वेग म्हणतात.
म्हणजेच वेग = चाल + दिशा..
वेग = विस्थापन/काळ
क्रिकेटच्या सामन्यात गोलंदाजीचा वेग रडार प्रणालीद्वारे काढला जातो.
चाल व वेग दोघांचेही SI पद्धतीत m/s (मीटर प्रती सेकंद) हेच एकक आहे. व CGS पद्धतीत cm/s हे एकक आहे.
चाल अंतराशी संबंधित आहे तर वेग विस्थापनाशी संबंधीत आहे.
गती सरळ रेषेत असेल तर वेग आणि चाल यांचे मूल्य सारखेच असते.
अन्यथा चाल ही गतीपेक्षा अधिक मूल्य असणारी राशी आहे.
चाल व वेग यांच्यावर आधारित गतीचे प्रमुख दोन प्रकार पडतात.
1.एकरेषीय एकसमान गती (Linear Uniform Motion)
- एकरेषीय नैकसमान गती (Linear Non-uniform Motion)
एकरेषीय एकसमान गती (Linear Uniform Motion)
ज्या गतीमध्ये वस्तू समान कालावधीत समान अंतर कापत असेल तर त्यास “एकसमान गती” म्हणतात.
उदा : एखादी वस्तू पहिल्या 30 सेकंदात 100 मीटर अंतर कापत असेल तर ती दुसऱ्या 30 सेकंदात तेवढेच अंतर पार पाडते.
म्हणजे एकसमान गतीमध्ये चाल स्थिर (Constant) राहते.
एकरेषीय नैकसमान गती (Linear Non-uniform Motion)
ज्या गतीमध्ये वस्तू कालांतराने स्वतःची चाल बदलते व समान कालावधीत वेगवेगळे अंतर कापते त्यास नैकसमान गती म्हणतात.
उदा : एखादी वस्तू पहिल्या 30 सेकंदात 100 मीटर अंतर कापते तर तीच वस्तू दुसऱ्या 30 सेकंदात 100 मीटर पेक्षा जास्त किंवा कमी अंतर कापते.
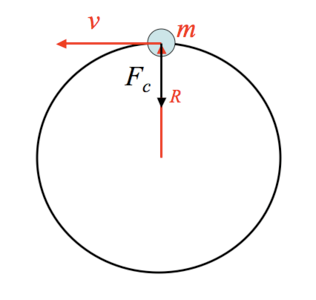
एकसमान वर्तुळाकार गती (Uniform Circular Motion)
आपण एकरेषीय गती पाहिली. जर एखादी वस्तू वर्तुळाकार मार्गाने सारख्याच वेळेत सारखेच अंतर कापत असेल तर त्यास एकसमान “वर्तुळाकार गती” असे म्हणतात.
वैशिष्ट्ये
या गतीत चाल सारखीच असते. परंतु वेग बदलत जातो कारण वर्तुळाकार फिरणारी वस्तू प्रत्येक क्षणी दिशा बदलते .
वेग = अंतर/काल = परीघ/काळ = 2πr/t
T = 3.14, r = वर्तुळाची त्रिज्या, 1 = काळ
ही वस्तू फिरताना नेहमीच केंद्रकाकडे आकर्षित होऊन फिरते, त्या आकर्षण बलास Centripetal Force असे म्हणतात.
उदा. :
- पृथ्वीची सूर्याभोवती गती.
- इलेक्ट्रॉनची केंद्राभोवती गती.
- वळणाऱ्या रस्त्यावर वाहनाची गती.
- चंद्राची पृथ्वीभोवती गती.
त्वरण (Acceleration)
वेगाचा दर म्हणजे त्वरण होय.
म्हणजेच एखाद्या वस्तूचा वेग व काळ यांचा संबंध म्हणजे “त्वरण” होय.
याला वेग बदलाचा दर म्हणतात.

त्वरण = v-u/t = वेग बदल / काळ = अंतिम वेग – आरंभ वेग /एकूण कालावधी
a= त्वरण, v = अंतिम वेग,
U= सुरुवातीचा वेग
- SI पद्धतीत त्वरणाचे एकक = m/s2
- CGS पद्धतीत त्वरणाचे एकक = cm/s:
जर समान कालावधीत गतीमध्ये समान बदल होत असेल तर त्वरण एकसमान राहते.
जर एखाद्या वस्तूची चाल ही स्थिर असेल तर त्या वस्तूचे त्वरण शून्य असते. (एकसमान गती)
त्वरण ऋण, धन व शून्य असू शकते.
- वेग वाढला तर धन त्वरण,
- वेग कमी झाला तर ऋण त्वरण/मंदन/अवत्वरण,
- वेगात बदल नाही झाला तर शून्य त्वरण.
गतिविषयक समीकरणे (Equation of Motion)
अ) वेग-काल संबंधीचे समीकरण (पहिले समीकरण)
V = u + at
v = अंतिम वेग,
u = सुरुवातीचा वेग,
a = त्वरण,
त्वरण (a) = v -u/t, at =v-u.
V = u + a t
ब) स्थिती-काल संबंधाचे समीकरण (दुसरे समीकरण)
s = UT + ½ at2
S=अंतर,
u = आरंभ वेग,
v= अंतिम वेग
t=. काळ
क) स्थिती-वेग संबंधाचे समीकरण (तिसरे समीकरण)
V2= u2 + 2as
6, अदिश व सदिश राशी (Scalar & Vector)
अ) अदिश राशी (Scalar Quantity)
जी राशी फक्त परिमाणाच्या (Magnitude) साहाय्याने दर्शविता येते त्यांना “अदिश राशी” असे म्हणतात,
म्हणजेच या राशीला दिशा नसते.
उदा. : अंतर, चाल, वस्तुमान, आकार, घनता, वेळ
व) सदिश राशी (Vector Quantity)
जी राशी दर्शविण्यासाठी परिमाण व दिशा (Magnitude & Direction) हे दोन्हीही लागतात त्या राशीला “सदिश राशी” असे म्हणतात.
ही राशी दर्शविताना डोक्यावर बाण काढतात.
उदा.: त्वरण, वेग, विस्थापन, बल इ.
